Laser drilling
Manufacturers of turbine engines for aircraft propulsion and for power generation have benefited from the productivity of lasers for drilling small (0.3–1 mm diameter typical) cylindrical holes at 15–90° to the surface in cast, sheet metal and machined components. Their ability to drill holes at shallow angles to the surface at rates of between 0.3 to 3 holes per second has enabled new designs incorporating film-cooling holes for improved fuel efficiency, reduced noise, and lower NOx and CO emissions.
Incremental improvements in laser process and control technologies have led to substantial increases in the number of cooling holes used in turbine engines. Fundamental to these improvements and increased use of laser drilled holes is an understanding of the relationship between process parameters and hole quality and drilling speed.
Contents |
Theory
Following is a summary of technical insights about the laser drilling process and the relationship between process parameters and hole quality and drilling speed.
Physical phenomena
Laser drilling of cylindrical holes in turbine engine components generally occurs through melting and vaporization (also referred to as ‘ablation’) of the workpiece material through absorption of energy from a focused laser beam.
The energy required to remove material by melting is about 25% of that needed to vaporize the same volume, so a process that removes material by melting is generally favored.
Whether melting or vaporization is more dominant in a laser drilling process depends on many factors, with laser pulse duration and energy playing an important role. Generally speaking, ablation dominates when a Q-switched Nd:YAG laser is used. On the other hand, melt expulsion, the means by which a hole is created through melting the material, dominates when a flashtube pumped Nd:YAG laser is used. A Q-switched Nd:YAG laser normally has pulse duration in the order of nanoseconds, peak power on the order of ten to hundreds of MW/cm2, and a material removal rate of a few micrometres per pulse. A flash lamp pumped Nd:YAG laser normally has a pulse duration on the order of hundreds of microseconds to a millisecond, peak power in the order of sub MW/cm2, and material removal rate of ten to hundreds of micrometers per pulse. For machining processes by each laser, ablation and melt expulsion typically coexist.
Melt expulsion arises as a result of the rapid build-up of gas pressure (recoil force) within a cavity created by evaporation. For melt expulsion to occur, a molten layer must form and the pressure gradients acting on the surface due to vaporization must be sufficiently large to overcome surface tension forces and expel the molten material from the hole (Figure 1).[1]
The “best of both worlds” is a single system capable of both “fine” and “coarse” melt expulsion. “Fine” melt expulsion produces features with excellent wall definition and small heat-affected zone while “coarse” melt expulsion, such as used in percussion drilling and trepanning, removes material quickly.
The recoil force is a strong function of the peak temperature. The value of Tcr for which the recoil and surface tension forces are equal is the critical temperature for liquid expulsion. For instance, liquid expulsion from titanium can take place when the temperature at the center of the hole exceeds 3780 K.
In early work (Körner, et al., 1996),[2] the proportion of material removed by melt expulsion was found to increase as intensity increased. More recent work (Voisey, et al., 2000)[3] shows that the fraction of the material removed by melt expulsion, referred to as melt ejection fraction (MEF), drops when laser energy further increases. The initial increase in melt expulsion on raising the beam power has been tentatively attributed to an increase in the pressure and pressure gradient generated within the hole by vaporization.
It is generally agreed that a better finish can be achieved if the melt is ejected in “fine” droplets. Figure 2 shows droplet size distribution of a Ni–based superalloy drilled by a Nd:YAG laser under; 2.5 J / 0.5 ms, 1.4 J / 0.5 ms and 2.5 J / 0.9 ms pulse energy / duration. Generally speaking, droplet size decreases with increasing pulse intensity. This is due to the increased vaporization rate and thus a thinner molten layer. For the longer pulse duration, the greater total energy input helps form a thicker molten layer and results in the expulsion of correspondingly larger droplets.[4]
Previous Models
Chan and Mazumder (1987)[5] developed a 1-D steady state model to incorporate liquid expulsion consideration but the 1-D assumption is not suited for high aspect ratio hole drilling and the drilling process is transient. Kar and Mazumder (1990)[6] extended the model to 2-D, but melt expulsion was not explicitly considered. A more rigorous treatment of melt expulsion has been presented by Ganesh, et al. (1997),[7] which is a 2-D transient generalized model to incorporate solid, fluid, temperature, and pressure during laser drilling, but it is computationally demanding. Yao, et al. (2001)[8] developed a 2-D transient model, in which a Knudsen layer is considered at the melt-vapor front, and the model is suited for shorter pulse and high peak power laser ablation.
Laser energy absorption and melt-vapor front
At the melt-vapor front, the Stefan boundary condition is normally applied to describe the laser energy absorption (Kar and Mazumda, 1990; Yao, et al., 2001).
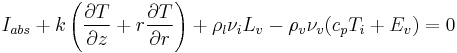 (1)
(1)
where 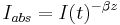 is the absorbed laser intensity, β is the laser absorption coefficient depending on laser wavelength and target material, and I(t) describes temporal input laser intensity including pulse width, repetition rate, and pulse temporal shape. k is the heat conductivity, T is the temperature, z and r are distances along axial and radial directions, p is density, v the velocity, Lv the latent heat of vaporization. The subscripts l, v and i denote liquid phase, vapor phase and vapor-liquid interface, respectively.
is the absorbed laser intensity, β is the laser absorption coefficient depending on laser wavelength and target material, and I(t) describes temporal input laser intensity including pulse width, repetition rate, and pulse temporal shape. k is the heat conductivity, T is the temperature, z and r are distances along axial and radial directions, p is density, v the velocity, Lv the latent heat of vaporization. The subscripts l, v and i denote liquid phase, vapor phase and vapor-liquid interface, respectively.
If the laser intensity is high and pulse duration is short, the so-called Knudsen layer is assumed to exist at the melt-vapor front where the state variables undergo discontinuous changes across the layer. By considering the discontinuity across the Knudsen layer, Yao, et al. (2001) (Figure 3) simulated the surface recess velocity Vv distribution, along the radial direction at different times, which indicates the material ablation rate is changing significantly across the Knudsen layer.
Melt expulsion
After obtaining the vapor pressure pv, the melt layer flow and melt expulsion can be modeled using hydrodynamic equations (Ganesh et al.,1997). As seen in Figure 4, melt expulsion occurs when the vapor pressure is applied on the liquid free surface which in turn pushes the melt away in the radial direction. In order to achieve fine melt expulsion, the melt flow pattern needs to be predicted very precisely, especially the melt flow velocity at the hole’s edge. Thus, a 2-D axisymmetric transient model is used and accordingly the momentum and continuity equations used.
Ganesh’s model for melt ejection is comprehensive and can be used for different stages of the hole drilling process. However, the calculation is very time consuming and Solana, et al. (2001),[9] presented a simplified time dependent model that assumes that the melt expulsion velocity is only along the hole wall, and can give results with a minimum computational effort.
As shown in Figure 5, the liquid will move upwards with velocity u as a consequence of the pressure gradient along the vertical walls, which is given in turn by the difference between the ablation pressure and the surface tension divided by the penetration depth x.
Assuming that the drilling front is moving at a constant velocity, the following linear equation of liquid motion on the vertical wall is a good approximation to model the melt expulsion after the initial stage of drilling.
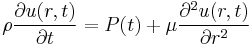 (2)
(2)
where p is the melt density, μ is the viscosity of the liquid, P(t)=(ΔP(t)/x(t)) is the pressure gradient along the liquid layer, ΔP(t) is the difference between the vapor pressure Pv and the surface tension 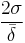 .
.
Pulse shape effect
Roos (1980)[10] showed that a 200 µs train consisting of 0.5 µs pulses produced superior results for drilling metals than a 200 µs flat shaped pulse. Anisimov, et al. (1984)[11] discovered that process efficiency improved by accelerating the melt during the pulse.
Grad and Mozina (1998)[12] further demonstrated the effect of pulse shapes. A 12 ns spike was added at the beginning, middle, and the end of a 5 ms pulse. When the 12 ns spike was added to the beginning of the long laser pulse, where no melt had been produced, no significant effect on removal was observed. On the other hand, when the spike was added at the middle and the end of the long pulse, the improvement of the drilling efficiency was 80 and 90%, respectively. The effect of inter-pulse shaping has also been investigated. Low and Li (2001)[13] showed that a pulse train of linearly increasing magnitude had a significant effect on expulsion processes.
Conclusion
Manufacturers are applying results of process modeling and experimental methods to better understand and control the laser drilling process. The result is higher quality and more productive processes that in turn lead to better end products such as more fuel efficient and cleaner aircraft and power generating turbine engines.
See also
References
- ^ Basu, S. and T. DebRoy, "Liquid Metal Expulsion During Laser Irradiation." J. Appl. Phys., 1992. 72: p. 3317-3322.
- ^ Körner, C., R. Mayerhofer, M. Hartmann and H. Bergmann, "Physical and Material Aspects in Using Visible Laser Pulses of Nanosecond Duration for Ablation." Appl. Phys. A, 63 (1996), pp. 123–31.
- ^ Voisey, K.T., C.F. Cheng, and T.W. Clyne. "Quantification of Melt Ejection Phenomena during Laser Drilling in Laser-Solid Interactions for Materials Processing." MRS, 2000. San Francisco.
- ^ Voisey, K.T., J.A. Thompson, T.W. Clyne, Damage caused during laser drilling of thermal spray TBC superalloy substrates." ICALEO 2001, Jacksonville FL, 14-18th October 2001.
- ^ Chan, C. and J. Mazumder, "One-Dimensional Steady State Model for Damage by Vaporization and Liquid Expulsion Due to Laser-material Interaction." J. Appl. Phys., 1987. 62(11): p. 4579 -86.
- ^ Kar, A., and Mazumder, J., 1990, "Two-Dimensional Model for Material Damage due to Melting and Vaporisation during Laser Irradiation." J. Appl. Phys., 68, pp. 3884–3891.
- ^ Ganesh, R. K., A. Faghri and Y. Hahn, "A Generalized Thermal Modeling for Laser Drilling Process: 1. Mathematical Modeling and Numerical Methodology." Int. J. Heat Mass Transfer, 40 (1997), pp. 3351–3360.
- ^ Yao, Y. L., Zhang, W.W., Chen, K., 2001, "Modeling and Analysis of UV Laser Micromachining of Copper." Int. J. Adv. Manuf. Technol., Vol. 18, pp. 323–331.
- ^ Solana, P., P. Kapadia, J. Dowden, W.S.O. Rodden, S.S. Kudesia, D.P. Hand and J.D.C. Jones, "Time Dependent Ablation and Liquid Ejection Process During the Laser Drilling of Metals." Optics Communications, 2001. 191: p. 97-112.
- ^ Roos, S. O., "Laser drilling with different pulse shapes." J Appl Phys 1980; 51:5061.
- ^ Anisimov, V.N., et al., Appl. Opt. 23 1984 18.
- ^ Grad, L., and J. Mozina, "Laser Pulse Shape influence on Optically Induced Dynamic Processes." Appl. Surf. Sci., 127-129 (1998), pp. 999–1004.
- ^ Low, D. K. Y., L. Li and P. J. Byrd, "The Influence of Temporal Pulse Train Modulation during Laser Percussion Drilling, Optics and Lasers in Engineering." 35 (2001), pp. 149–164.